rupeshtiwari/coding-examples-interview-coding-datastructure-algorithm-in-javascript

BranchesTags

Repository files navigation

Coding interview question answers in JavaScript for Facebook, Amazon, Google, Microsoft or any company. Find all notes and Coding exercises for this repo here

  • Remember: Run through your code not through the algorithm while executing test.
  • While solving problem: give yourself difficult values like use 7-8 elements of array not just 3 elements array. [1,2,3] instead use [12,34,22,51,6,96,43,8]
  • While executing your code always start with very easy example [2,3,1]

  • Download or clone in local machine.

  • Run npm ci

  • Then run individual file to see result on console.

  • You should use node filename in console to see results.

    View all of the coding exercises and answers

Make sure you know Computer science basic data structures. Also you should be aware of fundamental algorithms.

Once they give you problem, don't start coding. Ask clarifying questions to make sure you understand the problem.

Example:

  • Will there be null/empty values on input?
  • Will all numbers in a binary tree integers?
  • Computer Science Concepts
  • DataStructure
  • Algorithms
  • Big O Time
  • Big O Space
  • Recursion
  • Memoization / Dynamic Programming

Learn Big O. Make sure you give what would be the runtime complexity and memory complexity.

  • Array.push() is O(1) constant time complexity
  • string.indexOf() search is O(n) linear time complexity
  • for loop O(n) linear time complexity

Iterative functions take no extra memory and therefore, memory complexity is constant O(1).

Recursive functions take extra on the stack therefore, memory complexity is lograrithmic O(logn)

Factorial Simple Recursion

Factorial Simple Recursion

Recursive Factorial Simulation

Recursive Factorial Simulation

Recursive Factorial Time complexity O(n)

Recursive Factorial Time complexity

Recursive Factorial Space complexity is O(n)

Recursive Factorial Space complexity

  • Array
  • Hash Table
  • Linked List
  • Stack
  • Queue
  • Tree
  • Tries
  • Graphs
  • Heaps
  • Vectors
  • Merge sort
  • Quick sort
  • Breadth-first search
  • Depth-first search
  • Binary Search

Arrays can store a fixed number of elements, whereas a collection stores object dynamically so there is no size restrictions it grows and shrinks automatically.

  • Insert at the end (push) is efficient.
  • Insert at in between is not efficient.

Given a sorted array of integers, return the index of the given key. Return -1 if the key is not found.

Run below script

node .\src\arrays\binary-search.js

Given a large array of integers and a window of size w, find the current maximum value in the window as the window slides through the entire array.

Linked lists are dynamic data structure and memory is allocated at run time. They don't store data contiguously rather they use link to point to other elements.

Performance wise linked lists are slower than arrays because there is no direct access to linked list elements.

Suppose we have an array that contains following five elements 1, 2, 4, 5, 6. We want to insert a new element with value “3” in between “2” and “4”.

You have to copy 1,2 in new array then insert 3 and copy rest of the values. Runtime complexity and memory complexity is very high.

Therefore, we use linked list to store 1-6 and we can easily insert 3 in between 2 and 4.

The linked list is a list of items, called nodes. Nodes have two parts, value part and link part. Value part is used to stores the data. The link part is a reference, which is used to store addresses of the next element in the list.

  • Head: Head is a reference that holds the address of the first node in the linked list.
  • Nodes: Items in the linked list are called nodes.
  • Value: The data that is stored in each node of the linked list.
  • Link: Link part of the node is used to store the reference of other node.

class LinkedListNode {
  constructor(data) {
    this.data = data;
    this.next = null;
  }
}

Below are the types of LinkedList:

  • Singly Linked List

  • Doubly Linked List

  • Circular Linked List

Implement a LinkedList:

The newly created node will become head of the linked list. · Size of the list is increased by one.

We’re given the pointer/reference to the head of a singly linked list, reverse it and return the pointer/reference to the head of the reversed linked list.

Problem Solving steps

Running program output

Depth First Search (DFS) uses a stack for storing the nodes that it is visiting.

var stack = [1, 2, 3, 4];
stack.pop(); // 4 , stack [1,2,3]
stack.pop(); // 3 , stack [1,2]
stack.pop(); // 2 , stack [1]
stack.pop(); // 1 , stack [ ]

Breadth First Search (BFS) uses a queue for storing the nodes that it is visiting.

var queue = [];

queue.push(1); //   queue [1]
queue.push(2); //   queue [1,2]
queue.push(3); //   queue [1,2,3]
var queue = [1, 2, 3, 4];
queue.shift(); // 1 , queue [2,3,4]
queue.shift(); // 2 , queue [3,4]
queue.shift(); // 3 , queue [4]
queue.shift(); // 4 , queue [ ]

A tree has hierarchical data and it has nodes. It is a type of graph. Each node (except root) has exactly on parent and zero or more children. A tree is acyclic meaning it has no cycles: "a cycle is a path [AKA sequence] of edges and vertices wherein a vertex is reachable from itself". Therefore, a tree is also called as Directed Acyclic Graph (DAG).

  • Root: top node of tree is called root and has no parent and has no incoming edges.
  • Node: every node has parent ( except root ) and 0 or more children's.
  • Edge: used to connect two nodes.
  • Path: A path is an ordered list of nodes that are connected by edges.
  • Leaf: A leaf node is a node that has no children.
  • Height of the tree: The height of a tree is the number of edges on the longest path between the root and a leaf.
  • The level of node: The level of a node is the number of edges on the path from the root node to that node.
  • Children: Nodes that have incoming edges from the same node to be said to be the children of that node.
  • Parent: Node is a parent of all the child nodes that are linked by outgoing edges. - Sibling: Nodes in the tree that are children of the same parent are called siblings.
  • Ancestor:  A node reachable by repeated moving from child to parent.

If you want to store hierarchical data use Tree.

You should know about Binary Tree and Binary Search Tree.

In BFS algorithm, a graph is traversed in layer-by-layer fashion. point. The queue is used to implement BFS.

Example: Suppose you have given a tree structure and asked to calculate the average of numbers at each level.

The DFS algorithm we start from starting point and go into depth of graph until we reach a dead end and then move up to parent node (Backtrack). The stack is used to implement DFS.

  • Strategy: Recursive
  • Time Complexity: O(n logn)
  • Space Complexity: O(n logn)
  • Use Recursive Call Stack while coding.

BFSDFS
Search level by levelSearch from root to the leaf
Uses Queue to sortUses Stack to sort
Time complexity: SlowTime complexity: Fast
Where to use: solution is not far from the root of the tree,If the tree is very deep and solutions are rare, If solutions are frequent but located deep in the tree,Where to use: tree is very wide
Time Complexity: O(V+E)Time Complexity: O(V+E)

A binary tree is a type of tree in which each node has at most two children (0, 1 or 2) which are referred as left child and right child.

A Minimal Binary Tree has about the same number of nodes on the left of each node as on the right.

In Binary Search Tree nodes are:

  • The key in the left subtree is less than the key in its parent node.
  • The key in the right subtree is greater or equal the key in its parent node.

Checkout Binary Search Tree Visualization here.

BSTs get an average case of O(log n) on gets, adds, and deletes, but they can have a worst case of O(n) if you do something like add a sorted list to a BST. Go ahead, do a BST then add [1,2,3,4,5] to it.

Below image showing how to add [3, 7, 4, 6, 5, 1, 10, 2, 9, 8] in BST.

Binary Search Algorithm

Binary Search can be done both in iterative or recursive way.

Binary Search tree has left sub tree which is less than or equal to root. And right subtree which is strictly greater than the root.

Below image is not a BST

Simulating Recursive Binary Search for an existing number in a sorted increasing order unique integer array.

Simulating Recursive Binary Search for an non-existing number in a sorted increasing order unique integer array.

Trie is a tree, in which we store only one character at each node. This final key value pair is stored in the leaves.

Trie is also suitable for solving partial match and range query problems.

Each node in the heap follows the rule that the parent value is greater than its two children are.

There are two types of the heap data structure:

  • Max heap: each node should be greater than or equal to each of its children.
  • Min heap: each node should be smaller than or equal to each of its children.

A heap is a useful data structure when you want to get max/min one by one from data.

It is just like a dictionary or key value pair.

Graph represents network. It has Nodes, Vertices and Edges.

Implement Graph Question Implement Graph Answer

When you want to find all possible routes between airports then you want to use BFS. Find all possible routes from PHX to BKK. Also then you can decide which path is the shortest one.

Question Answer Source Code: Find all possible routes between 2 airports using BFS

![ ]((https://i.imgur.com/DrWF78t.png)

Question Answer Source Code: Find shortest route between 2 airports using DFS

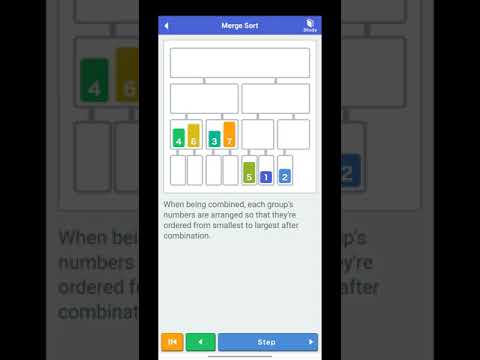
Browser's JavaScript Engine (Array..sort) uses merge sort maximum time. Runtime complexity O(n logn), Memory complexity O(n) because we have to create new list. It uses divide-and-conquer algorithm! and also it is recursive.

https://www.youtube.com/watch?v=UxnyImctVzg

Merge Sort Algorithm

Merge Sort Algorithm

Merge Sort Algorithm Simulation

Merge Sort Algorithm Simulation

Merge Sort Implementation Visualization:

Merge Sort Algorithm Simulator

See the Pen Merge Sort In-place Answer by Rupesh Tiwari (@rupeshtiwari) on CodePen.

2 sorted arrays find the median element. Median is the middle index its not an average of values in an sorted array.

So in order to find median we can use the stich algorithm since arrays are already sorted. Then we can find the middle index.

Find Median Values Question & Answer

When Browser's are not using Merge sort they most of the time use Quick sort variations. Most powerful sorting algorithm

Quick sort Algorithm

Quick sort Algorithm

Pseudo Code for Quick Sort Algorithm

Pseudo Code for Quick Sort Algorithm

Quick Sort Algorithm Simulation

Quick Sort Algorithm Simulation

Quick Sort Partition Algorithm

Quick Sort Partition Algorithm

Quick Sort Partition Algorithm Simulation

Quick Sort Partition Algorithm Simulation

Implement Quick Sort Algorithm Question

Implement Quick Sort Question

Quick Sort Answer with extra Array and Space complexity is O(n)

Implement Quick Sort Answer

Quick Sort Answer with in-place partition and Space complexity O(1) the most Efficient algorithm

Implement in-place algorithm for Quick Sort Answer

In Quick sort we do not create auxiliary arrays. Therefore, it is good choice for Array to use quick sort. However in merge sort we create 2 auxiliary arrays. Therefore, linked list is a good choice.

XOR represents the inequality function, i.e., the output is true if the inputs are not alike otherwise the output is false. A way to remember XOR is "must have one or the other but not both". XOR can also be viewed as addition modulo 2.

Find how many different numbers in the array.

Input =[3, 5, 6, 3, 3 , 9, 5]

answer = 4

There are 4 values 3,5, 6,9.

x = 0;
array.forEach((num) => (x ^= num));
return x;

^= XOR assignment operator.

Example create an array containing numbers from 0 to 9. [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

var y = new Array.from(Array(10).keys());

Answer: 9

1,000,000,000 = 1 Billion

Answer: 6

1,000,000 = 1 Million

Divide two integers without using '/' (division) or '*' (multiplication) operators.

node .\src\math-and-stats\integer-division.js

const x = new Array(4).fill(new Array(4).fill(0));

const map = new Map();
// insert
map.set('key', 'value');

// get
map.get('key');

// remove
map.delete('key');

// check key exist
map.has('key');

// size
map.size;

By default array.sort does not work you must pass delegate method.

var a = [23, 4, 2, 155, 43];
a.sort();
// output: [155, 2, 23, 4, 43] Not sorted at all.

In order to sort in ascending order you must pass delegate method.

Ascending Order Sorting

var a = [23, 4, 2, 155, 43];
a.sort((a, b) => a - b);
// output: [2, 4, 23, 43, 155]

Descending Order Sorting

var a = [23, 4, 2, 155, 43];
a.sort((a, b) => b - a);
// output: [155, 43, 23, 4, 2]

An integer is a whole number that can be either greater than 0, called positive, or less than 0, called negative. Zero is neither positive nor negative.

Letters asci code starts from 96 to 122.

  • charCodeAt() gives the ascii code.
  • String.fromCharCode(code) converts code to string.
const letter = 'A';
const newKey = (letter.charCodeAt() + 3) % 122;
const result = String.fromCharCode(newKey);
console.log(result); //"D"
Math.abs(-4); //4
Math.abs(2); //2

Slice does not mutate the original array. slice(index,count): Starts taking number from given index and go till given count.

Example of slice:

[20,39,48,58,16,36,48].slice(0,3) = [20,39,48]
[20,39,48,58,16,36,48].slice(3,7) = [58,16,36,48]

Math.floor(2.5) = 2
Math.floor(2.8) = 2
Math.floor(2.4) = 2
Math.round(2.5) = 3
Math.round(2.8) = 3
Math.round(2.4) = 2

Number.MAX_SAFE_INTEGER is the largest integer which can be used safely in calculations.

For example, Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2 is true — any integer larger than MAX_SAFE_INTEGER cannot always be represented in memory accurately. All bits are used to represent the digits of the number.

It is 16 digit number.

  • Number.MIN_SAFE_INTEGER = -9007199254740992
  • Number.MAX_SAFE_INTEGER = 9007199254740991

So basically ++i returns the value after it is incremented, while i++ return the value before it is incremented.

Moving bit/s towards the right side in binary number.

4>>2 = 16

x>>y means x/2^y divide x by 2 to the power of y.

Moving bit/s towards the left side in binary number.

4<<2 = 0

x<<y means x*2^y multiply x by 2 to the power of y.

Traverse by depth and collect all the numbers. And calculate average also.

Runtime Complexity O(logn) Space Complexity O(logn)

abstract data type (ADT) - ADT is defined as a user point of view of a data type and Does not talk about how exactly it will be implemented.

Trade off or invest some memory to improve run time complexity. Suppose use Has-table, set etc. to insert some of the calculations that you want to not repeat.

All Mandatory algorithm source code download here.

See the Pen Binary Search on Sorted Array Algorithm by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Merge Sort Algorithm by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Merge Sort Algorithm by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Quick Sort In-place Implementation: Answer by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Binary Tree Traversal by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Practice by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Practice by Rupesh Tiwari (@rupeshtiwari) on CodePen.

O(Log(n)) time | Space O(1)

For 1 insert operation, avg case is O(log(n)) and worst case is O(n) For n insert operations, avg case is O(n log(n)) and worst case is O(n^2)

O(log n) time | space O(1)

O(log(n)) time | O(1)

See the Pen Binary Search Tree Implementation by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Download solutions to Facebook Recruiting Portal Coding Interview Questions here.

Category: Graphs Difficulty: Easy

See the Pen Graph: DFS Question (easy) by Rupesh Tiwari (@rupeshtiwari) on CodePen.

See the Pen Graph: DFS Answer (easy) by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Graph Depth First Search Explanation

Answer Source Code Route Between Nodes

What is Minimal Tree?

Minimal Tree Simulation

Answer for Creating Minimal Tree Interview Question

Binary Search Tree (BST): is a binary tree in which for each node value of all the nodes in the left subtree is lesser or equal to the root node. And the values of all the nodes in the right subtree is greater than the root node.

In order to find a tree as BST we must define each node range that is its outer and inner bound values and iterate the tree and compare their ranges.

Is Binary Search Tree Algorithm

Is Binary Search Tree Algorithm Simulation

Is Binary Search Tree Coding Files

There are 3 conditions you should think:

Delete where there is no children

Delete node where there is 1 child

Delete node where there are 2 children

Delete 15 from BST

Question

See the Pen Delete node in BST Question by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Answer

See the Pen Delete node in BST Answer by Rupesh Tiwari (@rupeshtiwari) on CodePen.

<script async src="https://cpwebassets.codepen.io/assets/embed/ei.js"></script>

Case 1: If Node has right sub-tree. Then go deep to left-most node in right subtree or find the min in the right subtree.

Case 2: If Node has no right child then go to the nearest ancestor for which given node would be in the left tree.

Example: Find in-order successor of 12?

Example: Find in-order successor of 6?

Question

See the Pen Find In-order Successor in BST Question by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Answer

See the Pen Find In-order Successor in BST Answer by Rupesh Tiwari (@rupeshtiwari) on CodePen.

x to the power n Brute Force

x to the power n Brute Force

x to the power n using simple recursion un-optimized

x to the power n using simple recursion un-optimized

x to the power n using optimized recursion with multiple subproblems

x to the power n using optimized recursion with multiple subproblems

Modular Exponentiation is the remainder dividing up on Pow(x,n) by M.

Modular Exponentiation is the remainder dividing up on Pow(x,n) by M

[2,4,10,10,10,18,20] find first and last occurrence of number 10.

Finding first and last occurrence of a number in sorted array

[1,1,3,3,5,5,5,5,5,9,9,11] How many 5's here?

[11,12,15,18,2,5,6,8] how many times this sorted array is rotated? 💡 Hint: Once we find the pivot in this array then the index of the pivot will give you the rotation count.

Circularly sorted array means a rotated sorted array. Find index of 8 in [12, 14, 18, 21, 3, 6, 8, 9] array.

💡 Hint:

  • Brute Force => O(n) search each element of an array. Don't code for it.
  • Optimized => O(logN)

Circularly sorted array will have at least one half completely sorted. And the other half where you have the pivot element there elements will be also sorted after pivot element. Try Binary Search.

See the Pen Reverse Linked List: Answer by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Question Answer

See the Pen Find merge point of 2 linked list Answer by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Binary Search is used to solve 2 kinds of problems: 1- Search problems, find real numbers. 2- Optimization problems. Maximize element x keeping y minimum. Or minimize element x keeping y maximum.

Next you have to solve some basic binary search problems.

Below problems are lying under optimization problems. Just watch Book Allocation and Aggressive Cows videos (links are below) to understand optimization logic. Once you understood them after that for rest problems you need to apply same logic. Every iteration you reduce the search space by either maximizing or minimizing the solution.

It is useful for optimization problem. Below is the template for Greedy Algorithm.

getOptimal(items, n)
1- Initialize result as 0
2- while(all items are not considered) {
  i = selectAnItem()
  if(feasible(i))
    result = result +1;
}
3- return result;

See the Pen Min Coins by Rupesh Tiwari (@rupeshtiwari) on CodePen.

Note: Greedy Algorithms may not work always like Longest Path in Binary Tree.

Below are the standard problems solved by Greedy Algorithms. I have solved first 4 problems listed below:

https://codepen.io/collection/QWbzGB

  • Activity Selection
  • Fractional Knapsack
  • DIEHARD
  • DEFKIN
  • Job Sequencing
  • Huffman Coding
  • Prim's Algorithm
  • Kruskal's algorithm
  • Dijkstra's algorithm
  • Finding close to optimal solutions for NP Hard Problem like Travelling Salesman Problem

Merge 2 smallest and make one node. Next select 2 smallest and make one node. Repeat the merge process

Always select 2 minimum one is called as Greedy Algorithm. This is called as Optimal Merge Pattern Tree which is Greedy approach

- Take a LEFT then go extreme RIGHT to get predecessor of given node
- While going right update predecessor

- Take a RIGHT then go extreme LEFT to get successor of given node
- While going left update successor

Read the given constraints before coding and applying algorithm.

If N < 10^5 then you must solve the problem in run time complexity of O(N) or O(N log (n))

If constraints are given then read them and then decide complexity.

NRunTime Complexity
N < 4000 (10^3)O(n^n) or O( n log(n))
10^5O(n) or O(n log (n))
10^9O(log(n)) or O(1)

Examples:

https://www.codechef.com/problems/DECODEIT This should be done within O(n) or O(n log (n))

While learning DS solve problems for the same DS also. Example if you are learning string then solve the problems for the string.

  • Number Theory
  • Sorting Algorithms
    • Merge
    • Quick
  • Searching
    • Linear
    • Binary
  • Recursion & Backtracking
  • Greedy
  • Graph

Every topic finish 30 to 40 questions. For Array, String, Recursion and Graph do more than 50 questions.

Go to practice page: https://practice.geeksforgeeks.org/explore/?page=1

Every day do below:

  • 3 easy questions
  • 2 medium questions
  • 1 hard question
<script async src="https://cpwebassets.codepen.io/assets/embed/ei.js"></script> <script data-ad-client="ca-pub-1700383344966810" async="" src="https://pagead2.googlesyndication.com/pagead/js/adsbygoogle.js" data-checked-head="true"></script>

About

All you need to know about your coding interview includes algorithms, data structure, oops, design patterns, recursion, graph theory, tree traversal, combinatorial problems.

Topics

javascript algorithms graph-algorithms data-structures tree-structure designpatterns oops datastructures-algorithms recursion-exercises tree-traversal-algorithm combinatorial-problems

Resources

Readme
Activity

Stars

1 star

Watchers

1 watching

Forks

0 forks
Report repository

Releases

No releases published

Packages

No packages published

Languages